Экономический обзор

Средние величины и показатели вариации

Средняя величина - это обобщающая характеристика совокупности однотипных явлений по изучаемому признака.

Выбор средней определяется экономическим содержанием определенного показателя и исходных данных. В каждом конкретном случае применяется одна из средних величин:

. Арифметическая

. Гармоническая

. Квадратичная

. Геометрическая

Каждая из них может быть простой и взвешенной. Перечисленные средние относятся к классу степенных средних и определяются формулой (при различных значениях m):

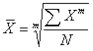
При m = -1 средняя гармоническая ; = 0 средняя геометрическая = 1 средняя арифметическая ;= 2 средняя квадратическая ;

Средняя арифметическая простая - это самая часто используемая средняя величина, которая получается, если подставить в общую формулу m=1. Средняя арифметическая простая имеет следующий вид:

где X - значения величин, для которых необходимо рассчитать среднее значение; N - общее количество значений X (число единиц в изучаемой совокупности).

Средняя арифметическая взвешенная вычисляется когда варианты встречаются не одинаковое число раз.

Число одинаковых значений и признаков в рядах распределения называется частотой или весом (f). Средняя арифметическая взвешенная имеет следующий вид:

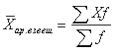
Для вычисления средней арифметической взвешенной необходимо:

. Каждую варианту умножить на вес признака (x*f)

. Найти сумму этих произведений

. Сумму произведений вариант

Средняя гармоническая простая применяется в тех случаях, когда вес каждого варианта =1, и когда индивидуальное значение обратного признака встречается по 1 разу. Средняя гармоническая простая обратная средней арифметической из обратных значений признака.

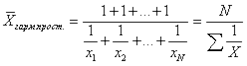
Средняя гармоническая простая применяется для расчета средней трудоемкости и средней производительности труда.

Средняя гармоническая взвешенная применятся, когда статистическая информация не содержит частой по отдельным вариантам совокупности, а представлена как их произведение, и когда имеются данные об индивидуальных значениях признака и общем объеме совокупности, но неизвестны частоты.

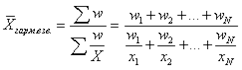
Средняя квадратическая простая применяется для расчета среднего диаметра стволов деревьев, клубней, труб и т.д. Т.е. она применятся для обобщения признаков, выраженных линейными мерами каких-либо площадей. Средняя квадратическая простая определяется путем деления суммы квадратов отдельных значений признаков на их число и извлечение из полученного частного квадратного корня.

Средняя квадратическая взвешенная применяется в том случае, если будет частота повторения признака.

Средняя геометрическая простая применяется в тех случаях, когда индивидуальное значение признака представляет собой относительные величины динамики. Вычисляется путем извлечения корня степени n из произведений отдельных значений признака.

Модой называется наиболее часто встречающаяся величинв признака. Определение моды зависит от того, в каком ряду представлен вальрирующий признак, если вальрирующий признак представлен в в идее дискретного ряда распределения, то для определения моды не требуется никаких вычислений. В таком ряду модой будет то значение признака, которое обладает наибольшей частотой. Если значение признака представлены в виде интервального вида, то мода определяется:

где Мо - мода;

ХНМо - нижняя граница модального интервала

;hМо - размах модального интервала (разность между его верхней и нижней границей);Мо - частота модальноого интервала;Мо-1 - частота интервала, предшествующего модальному;Мо+1 - частота интервала, следующего за модальным.

Медианой называется варианта, расположенная в середине вариационного ряда. Если ряд распределения дискретный и имеет нечетное число членов, то медианой будет варианта, находящаяся в середине упорядоченного ряда. А если упорядоченный ряд состоит из четного числа членов, то медианой будет средняя арифметическая двух вариант, расположенных в середине ряда. Медиану для интервального вариационного ряда рассчитывают:

где Ме - медиана;

НМе - нижняя граница медианного интервала;Ме - размах медианного интервала (разность между его верхней и нижней границей);Ме - частота медианного интервала;Ме-1 - сумма частот интервалов, предшествующих медианному.

Немного больше об экономике сегодня

Комплексная характеристика направлений социально-экономического развития Республики Дагестан
Актуальность выпускной работы. Современные российские экономические преобразования проходят сложные трансформационные изменения, целью которых является построение конкурентоспособной национальной экономики, выявление позитивных и негативных тенденций экономической и социальной эффективности трансформирующих меро ...

Инновационный механизм в совершенствовании производства
Современный этап в развитии российской экономике характеризуется интеграцией в мировую инфраструктуру. Мировые тенденции консолидации предприятий в течение последних лет привели к созданию крупнейших транснациональных корпораций, мощности которых сравнимы с мощностями ведущих мировых держав. Активное приобретение ...