Исследование цен и дивидендов
Умножаем матрицы:
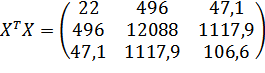
Умножаем матрицы, (XTY):
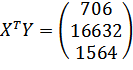
Находим обратную матрицу 
:
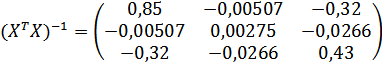
Вектор оценок коэффициентов регрессии равен:
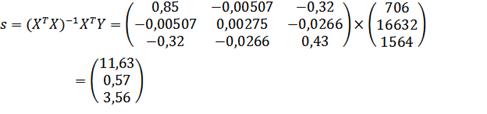
Уравнение регрессии (оценка уравнения регрессии):
где 
- цена акции, долл.,
- доходность капитала, %,
- уровень дивидендов, %.
При увеличении доходности капитала на 1%, цена акции увеличивается на 0,57 долл., а при увеличении уровня дивидендов на 1%, цена акции увеличивается на 3,56 долл.статистика
табл (n-m-1;α) = (19; 0.05) = 1.729
Находим стандартную ошибку коэффициента регрессии b0:
Статистическая значимость коэффициента регрессии b0 подтверждается.
Находим стандартную ошибку коэффициента регрессии b1:
Статистическая значимость коэффициента регрессии b1 подтверждается.
Находим стандартную ошибку коэффициента регрессии b2:
Статистическая значимость коэффициента регрессии b2 подтверждается.
Доверительный интервал для коэффициентов уравнения регрессии.
Определим доверительные интервалы коэффициентов регрессии, которые с надежность 90% будут следующими:
(bi - ti Sbi; bi + ti Sbi)
b0: (11.63 - 1.729 • 1.33; 11.63 + 1.729 • 1.33) = (9.34; 13.92)1: (0.57 - 1.729 • 0.0755; 0.57 + 1.729 • 0.0755) = (0.44; 0.7)2: (3.56 - 1.729 • 0.94; 3.56 + 1.729 • 0.94) = (1.93; 5.2)
8. Анализируем статистическую значимость коэффициентов множественного уравнения с надежностью 0,9.
Тесноту совместного влияния факторов на результат оценивает индекс множественной корреляции. В отличии от парного коэффициента корреляции, который может принимать отрицательные значения, он принимает значения от 0 до 1. Поэтому R не может быть использован для интерпретации направления связи. Чем плотнее фактические значения располагаются относительно линии регрессии, тем меньше остаточная дисперсия и, следовательно, больше величина индекса множественной корреляции.
Проверим статистическую значимость параметров уравнения множественной регрессии с надежностью 0.9. Вычислим коэффициент множественной корреляции:
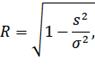
где 
- остаточная дисперсия для уравнения множественной регрессии;
- дисперсия эмпирических значений результативного признака.
|
№ |
| |||||
|
1 |
10 |
3,5 |
6,0 |
6,2 |
15,1 |
16,8 |
|
2 |
12 |
3,6 |
6,0 |
6,3 |
14,1 |
16,8 |
|
3 |
15 |
3,9 |
7,0 |
6,8 |
11,1 |
9,6 |
|
4 |
17 |
4,1 |
7,0 |
7,0 |
9,3 |
9,6 |
|
5 |
18 |
4,2 |
7,0 |
7,2 |
8,5 |
9,6 |
|
6 |
19 |
4,5 |
8,0 |
7,6 |
6,2 |
4,4 |
|
7 |
19 |
5,3 |
8,0 |
8,7 |
1,9 |
4,4 |
|
8 |
20 |
5,3 |
9,0 |
8,7 |
1,9 |
1,2 |
|
9 |
20 |
5,6 |
9,0 |
9,1 |
0,9 |
1,2 |
|
10 |
21 |
6,0 |
10,0 |
9,7 |
0,2 |
0,0 |
|
11 |
21 |
6,3 |
10,0 |
10,1 |
0,0 |
0,0 |
|
12 |
22 |
6,4 |
11,0 |
10,3 |
0,0 |
0,8 |
|
13 |
23 |
7,0 |
11,0 |
11,1 |
1,0 |
0,8 |
|
14 |
25 |
7,5 |
12,0 |
11,8 |
2,8 |
3,6 |
|
15 |
28 |
7,9 |
12,0 |
12,3 |
5,0 |
3,6 |
|
16 |
30 |
8,2 |
13,0 |
12,8 |
7,1 |
8,4 |
|
17 |
31 |
8,4 |
13,0 |
13,0 |
8,7 |
8,4 |
|
18 |
31 |
8,6 |
14,0 |
13,3 |
10,4 |
15,2 |
|
19 |
35 |
9,5 |
14,0 |
14,6 |
20,0 |
15,2 |
|
20 |
36 |
10,0 |
15,0 |
15,3 |
26,8 |
24,0 |
|
Сумма |
202,0 |
202,0 |
81,8 |
675,82 | ||
|
Среднее |
10,1 |
10,1 |
Немного больше об экономике сегодня
Максимизация дохода и минимизация издержек производства на примере ООО ТД Губернский
Одним
из главных показателей развития в стране нормальных рыночных отношений является
состояние рынка недвижимости в целом и его отдельных секторов в частности.
Рынок недвижимости является существенной составляющей в любой национальной
экономике, так как недвижимость - важнейшая часть национального богатства, на
...
Комплексный экономический анализ хозяйственной деятельности
1. Дать общую характеристику предприятия: год создания,
организационно-правовая форма, отраслевая принадлежность, вид деятельности, ее
масштабы, основные потребители продукции и другие сведения.
Примечание: название предприятия в интересах его собственников и
руководителей может быть изменено на любое другое ...